9.7. Sampling and Bootstrap Distributions of Parameters

9.7.1. Animated and Interactive Examples of Sampling Distributions

9.7.1.1. Sampling Distribution for Uniform \([0,10]\) Random Variable

U= stats.uniform(0,10, )
sampling_dist(U, 'Uniform $[0,10]$')

Once Loop Reflect

9.7.1.2. Sampling Distribution for Exponential (\(\lambda=1/5\)) Random Variable

E=stats.expon(scale=5)
sampling_dist(E, 'Exponential $\lambda=1/5$')

Once Loop Reflect

9.7.1.3. Sampling Distribution For Chi-Squared Random Variable with 6 Degrees of Freedom

C=stats.chi2(df=6 )
sampling_dist(C, "Chi-Sq dof=6")

Once Loop Reflect

9.7.1.4. Sampling Distribution for Binomial Random Variable with 100 Trials and Probability of Success 0.2

B = stats.binom(100, 0.2)
sampling_dist(B, "Binomial $(100,0.2)$")

Once Loop Reflect

9.7.1.5. Sampling Distribution for Average of Two Uniform Random Variables

U= stats.uniform(0,10)
sampling_dist(U, "Uniform $[0,10]$")

Once Loop Reflect

9.7.1.6. Sampling Distribution for Average of Two Normal Random Variables

N= stats.norm(3, 2)
sampling_dist(N, "Normal (0,1)")

Once Loop Reflect

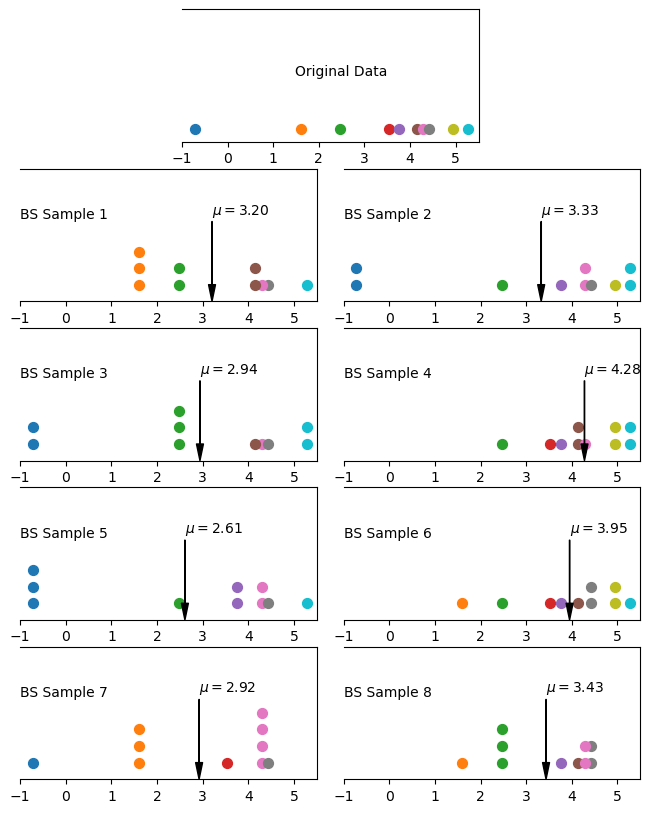
9.7.2. Code For Generating Images of Bootstrap Samples and Averages

The code for generating the image of bootstrap samples and averages was omitted from the text. I am including it here:

import matplotlib.gridspec as gridspec
gs = gridspec.GridSpec(5, 4)
#gs.update(wspace=0.5)

fig = plt.figure()
fig.set_dpi(100)
fig.set_size_inches(8, 10)
np.random.seed(23341)
N=stats.norm(3,2)
nvals = N.rvs(10)
nvals.sort()
#plt.scatter(nvals, 0.01 *np.ones(10), s=50)
ax1 = plt.subplot(gs[0, 1:3])
for i, val in enumerate(nvals):
  ax1.scatter(val, 0.01 , s=50, c='C'+str(i))
ax1.set_ylim(0, 0.1)
ax1.set_xlim(-1, 5.5)
np.random.seed(1234512)



#ax = plt.gca()
ax1.spines['left'].set_visible(False)
ax1.get_yaxis().set_visible(False)
ax1.text(2.5, 0.05, 'Original Data',horizontalalignment='center',)

#ax1 = plt.subplot(gs[0, :2], )
#ax3 = plt.subplot(gs[1, 1:3])


for sample in range(1,9):
  #bs = npr.choice(nvals, len(nvals))
  bs = npr.choice(np.arange(0,len(nvals)), len(nvals))
  bsvals = nvals[bs]
  counts={}
  for val in bs: 
    counts[val]=0
  xstart = 2*((sample+1) %2)
  ax = plt.subplot(gs[(sample+1) // 2, xstart:xstart+2])


  for val in bs:
    counts[val]+=1
    ax.scatter(nvals[val], 0.005*counts[val], s=50, c = 'C'+str(val))
    
  height = 0.01*(max(counts.values())+1)
  avg = bsvals.mean()
  #ax.scatter(avg, 0.005, marker='x')
  #ax.arrow(avg, height-0.01, 0, -height+0.01+0.005, head_width = 0.15, head_length=0.005 )
  ax.annotate(f'$\mu=${avg:0.2f}', xy=(avg, 0),  xycoords = 'data',
              xytext = (avg, 0.03),
              arrowprops=dict(facecolor='black', width=0.2, headwidth=5),
              horizontalalignment='left', verticalalignment='top',
  )
  ax.text(-1, 0.025, 'BS Sample '+str(sample),horizontalalignment='left',)
  
  ax.set_ylim(0, 0.04)
  ax.set_xlim(-1, 5.5)

  ax.spines['left'].set_visible(False)
  ax.get_yaxis().set_visible(False)

9.7.3. Terminology Review

Use the flashcards below to help you review the terminology introduced in this chapter. \(~~~~ ~~~~ ~~~~\)